Oke Math
Jumat, 07 Maret 2014
Kamis, 28 Maret 2013
SEGITIGA (TRIANGLE)
Pengertian Segitiga
Diberikan tiga buah titik A, B dan C yang tidak segaris. Titik A dihubungkan dengan B, titik B dihubungkan dengan titik C, dan titik C dihubungkan dengan titik A. Bangun yang terbentuk disebut segitiga (triangle).
gambar segitiga tersebut merupakan segitiga ABC.
Segitiga merupakan bangun datar yang mempunyai tiga sisi. Pada ∆ ABC di atas AB, BC dab AC disebut sisi segitiga ABC.
Ketiga sisi segitiga saling berpotongan dan membentuk sudut. Titik A, B, C disebut titik sudut (vertex).
Jadi sebuah segitiga memiliki tiga titik sudut, tiga sisi dan tiga sudut. Jumlah besar ketiga sudutnya adalah 180°.
Apa syarat garis yang dimiliki segitiga ABC?
1. AB + BC > AC
2. BC + AC > AB
3. AB + AC > BC
Jenis-Jenis Segitiga
1. Jenis-jenis Segitiga Ditinjau dari Sudut-sudutnya
Ditinjau dari susut-susutnya, segitiga dibedakan menjadi tiga, yaitu:
a. Segitiga lancip
Segitiga lancip adalah segitiga yang besar tiap sudutnya merupakan sudut lancip atau besar sudutnya antara 0° sampai dengan 90°.
b. Segitiga tumpul
Segitiga tumpul adalah segitiga yang salah
satu dari tiga sudutnya merupakan sudut tumpul atau besar sudutnya
antara 90° dan 180°.
c. Segitiga siku-siku
Segitiga siku-siku adalah segitiga yang salah satu sudutnya siku–siku atau besar sudutnya 90°.
2. Jenis-jenis Segitiga Ditinjau dari Panjang Sisi-sisinya
Ditinjau dari panjang sisi-sisinya, segitiga dibedakan menjadi tiga jenis, yaitu:
a. Segitiga Sembarang
Segitiga sembarang adalah segitiga yang ketiga sisinya berbeda panjangnya dan ketiga sudutnya berbeda besarnya.
b. Segitiga sama sisi
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang.
b. Segitiga sama kaki
Segitiga sama kaki adalah segitiga yang mempunyai dua sisi sama panjang.
3. Jenis-jenis Segitiga Ditinjau dari besar sudut dan Panjang Sisinya
Ditinjau dari besar sudut dan panjang sisinya, segitiga terbagi menjadi tujuh macam. Perhatikan table berikut ini :
Gambar segitiga:
1. Segitiga Lancip sama sisi
2. Segitiga Lancip sama kaki
3. Segitiga Tumpul sama kaki
4. Segitiga Siku-siku sama kaki
5. Segitiga Lancip sembarang
6. Segitiga Tumpul sembarang
7. Segitiga Siku-siku sembarang
Segitiga istimewa merupakan segitiga yang
memiliki sifat-sifat khusus (istimewa), baik mengenai hubungan panjang
sisi-sisinya maupun hubungan besar sudut-sudutnya. Yang merupakan
segitiga istimewa di antara jenis-jenis segitiga adalah :
– Segitiga siku-siku
– Segitiga siku-siku
- Segitiga sama kaki
– Segitiga sama sisi
JUMLAH SUDUT-SUDUT SEGITIGA
Perhatikan gambar berikut:
Gambar (i) menunjukkan sebuah segitiga lancip dari
karton yang dipotong ketiga sudutnya menurut garis putus-putus.
Selanjutnya potongan-potongannya diletakkan secara berdampingan pada
bidang datar, tanpa celah, dan saling menutup seperti terlihat pada
gambar (ii).
Dari bentuk tersebut terlihat bahwa ketiga sudut segitiga membentuk sudut lurus.
Jadi a + b + c = 180°
KELILING DAN LUAS SEGITIGA
Sebelum dibicarakan tentang Keliling dan Luas Segitiga, akan dibahas tentang alas dan tinggi (garis tinggi).
Garis Tinggi Segitiga
Garis tinggi adalah garis yang ditarik dari salah satu titik sudut dan tegak lurus dengan sisi di depannya.
Karena segitiga memiliki tiga buah titik sudut, maka setiap segitiga memiliki tiga buah garis tinggi.
Alas Segitiga
Setiap sisi segitiga dapat dipandang sebagai alas sebuah segitiga.
Perhatikan gambar berikut :
Sisi  AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi
AB disebut juga sebagai sisi c, karena letaknya di depan sudut C. Demikian juga sisi  BC dan
BC dan  AC disebut juga sebagai sisi a dan sisi b
AC disebut juga sebagai sisi a dan sisi b
Garis tinggi yang dibuat dari titik sudut C disebut tc, karena tegak lurus dengan alas atau sisi c atau  AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
AB. Demikian pula dengan garis tinggi yang dibuat dati titik sudut B dan A disebut tb dan ta.
Keliling Segitiga
Keliling sebuah bidang datar adalah jumlah panjang
sisi-sisi yang membatasi bidang datar tersebut. Jadi, keliling segitiga
adalah jumlah panjang ketiga sisinya.
Jika K menyatakan keliling segitiga ABC maka
K = AB + BC + AC
K = c + a + b
Jadi keliling segitiga dirumuskan sebagai berikut:
Luas Segitiga
Luas segitiga adalah setengah hasil kali panjang alas dan tingginya
Keterangan :
a = alas
t = tinggi
Solid Figure
--BANGUN RUANG--
Bangun ruang adalah bangun matematika yang mempunyai isi ataupun volume.
Bagian-bagian bangun ruang, antara lain:
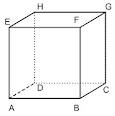
Ø Kubus mempunyai 6 sisi berbentuk persegi,
Ø Kubus mempunyai 12 rusuk yang sama panjang,
Ø Kubus mempunyai 8 titik sudut,
Ø Jaring-karing kubus berupa 6 buah persegi yang kongruen.
Rumus Luas Permukaan Kubus
L = 6 x r2
Keterangan :
L : luas permukaan
r : panjang rusuk
Rumus Volume Kubus
V = r3
Keterangan :
V = Volume
r = rusuk
BALOK
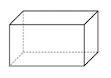
Ciri-ciri BALOK,antara lain:
Ø Balok merupakan bangun ruang yang dibatasi 6 persegi panjang dimana 3 persegi panjang kongruen,
Ø Balok mempunyai 6 sisi berbentuk persegi panjang,
Ø Balok mempunyai 3 pasang bidang sisi berhadapan yang kongruen,
Ø Balok mempunyai 12 rusuk,
Ø 4 buah rusuk yang sejajar sama panjang,
Ø Balok mempunyai 8 titik sudut,
Ø Jaring-jaring balok berupa 6 buah persegi panjang.
Rumus Luas Permukaan Balok
L = 2 x [ (p x l) + (p x t) + (l x t) ]
Keterangan:
t : tinggi balok
p : panjang balok
l : lebar balok
Rumus Volume Balok
V = p x l x t
Keterangan:
t : tinggi balok
p : panjang balok
l : lebar balok
PRISMA
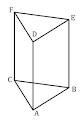
Ciri-ciri PRISMA, antara lain:
Ø Prisma merupakan bangun ruang yang alas dan atasnya kongruen dan sejajar,
Ø Rusuk prisma alas dan atas yang berhadapan sama dan sejajar,
Ø Rusuk tegak prisma sama dan sejajar,
Ø Rusuk tegak prisma tegak lurus dengan alas dan atas prisma,
Ø Rusuk tegak prisma disebut juga tinggi prisma,
Ø Prisma terdiri dari prisma segitiga dan prisma beraturan.
Ø Prisma segitiga mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen.
Ø Prisma segitiga mempunyai 5 sisi.
Ø Prisma segitiga mempunyai 9 rusuk
Ø Prisma segitiga mempunyai 6 titik sudut
Ø Jaring-jaring prisma segitiga berupa 2 segitiga, dan 3 persegi panjang.
Rumus Luas Permukaan Prisma Segitiga
L = Keliling ∆ x t x ( 2 x Luas ∆)
Volume Prisma Segitiga
V = Luas Alas x t
Keterangan :
L : luas permukaan
∆ : alas dan atas segitiga
t : tinggi prisma
V : Volume
Luas Alas : Luas ∆ = ( ½ a x t )
t : tinggi prisma
LIMAS
Ciri-ciri LIMAS,antara lain:
Ø Limas adalah bangun ruang yang mempunyai bidang alas segi banyak dan dari bidang alas tersebut dibentuk suatu sisi berbentuk segitiga yang akan bertemu pada satu titik,
Ø Nama limas ditentukan oleh bentuk alasnya,
Ø Limas beraturan yaitu limas yang alasnya berupa segi beraturan,
Ø Tinggi limas adalah garis tegak lurus dari puncak limas ke alas limas,
Ø Macam-macam bentuk limas, antara lain:
1. Limas segitiga ( alasnya berbentuk segitiga )
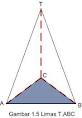
2. Limas segiempat ( alasnya berbentuk segi empat )
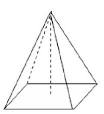
3. Limas segilima ( alasnya berbentuk segilima )
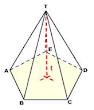
4. Limas segienam ( alasnya berbentuk segienam )
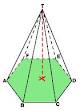
Rumus Luas Permukaan Limas
L = luas alas + luas selubung limas
Rumus Volume Limas
V = 1/3 ( luas alas x t )
Keterangan:
t : tinggi limas
TABUNG
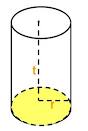
Ciri-ciri TABUNG, antara lain:
Ø Tabung merupakan bangun ruang berupa prisma tegak dengan bidang alas dan atas berupa lingkaran,
Ø Tinggi tabung adalah jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas,
Ø Bidang tegak tabung berupa lengkungan yang disebut selimut tabung,
Ø Jaring-jaring tabung tabung berupa 2 buah lingkaran dan 1 persegi panjang.
Rumus Luas Permukaan Tabung
L = 2 x ( π r2 ) + π d x t
Rumus Volume Tabung
V = 1/3 (luas alas x t)
Keterangan:
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi tabung
V : Volume
luas alas : π r2
KERUCUT
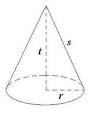
Ciri-ciri KERUCUT,antara lain:
Ø Kerucut merupakan bangun ruang berbentuk limas yang alasnya berupa lingkaran,
Ø Kerucut mempunyai 2 sisi,
Ø Kerucut tidak mempunyai rusuk,
Ø Kerucut mempunyai 1 titik sudut,
Ø Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga.
Rumus Luas Permukaan Kerucut
L = π r2 + π d xt
Rumus Volume Kerucut
V = 1/3 ( π r2 x t )
Keterangan:
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi kerucut
BOLA
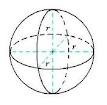
Ciri-ciri BOLA, antara lain:
Ø Bola merupakan bangun ruang berbentuk setengah lingkaran diputar mengelilingi garis tengahnya,
Ø Bola mempunyai 1 sisi dan 1 titik pusat,
Ø Sisi bola disebut dinding bola,
Ø Bola tidak mempunyai titik sudut dan rusuk,
Ø Jarak dinding ke titik pusat bola disebut jari-jari,
Ø Jarak dinding ke dinding dan melewati titik pusat disebut diameter.
Rumus Luas Permukaan Bola
L = 4 π r2
Rumus Volume Bola
V = 4/3 π r3
Keterangan:
L : luas permukaan
V : Volume
r : jari-jari bola
π : 22/7 atau 3,14
Bangun ruang adalah bangun matematika yang mempunyai isi ataupun volume.
Bagian-bagian bangun ruang, antara lain:
- Sisi: bidang pada bangun ruang yang membatasi antara bangun ruang dengan ruangan di sekitarnya.
- Rusuk: pertemuan dua sis yang berupa ruas garis pada bangun ruang.
- Titik sudut: titik hasil pertemuan rusuk yang berjumlah tiga atau lebih
- Kubus
- Balok
- Prisma
- Limas
- Kerucut
- Tabung
- Bola

Ciri-ciri KUBUS, antara lain :
Ø Kubus merupakan bangun ruang dengan 6 sisi sama besar (kongruen),Ø Kubus mempunyai 6 sisi berbentuk persegi,
Ø Kubus mempunyai 12 rusuk yang sama panjang,
Ø Kubus mempunyai 8 titik sudut,
Ø Jaring-karing kubus berupa 6 buah persegi yang kongruen.
Rumus Luas Permukaan Kubus
L = 6 x r2
Keterangan :
L : luas permukaan
r : panjang rusuk
Rumus Volume Kubus
V = r3
Keterangan :
V = Volume
r = rusuk
BALOK

Ciri-ciri BALOK,antara lain:
Ø Balok merupakan bangun ruang yang dibatasi 6 persegi panjang dimana 3 persegi panjang kongruen,
Ø Balok mempunyai 6 sisi berbentuk persegi panjang,
Ø Balok mempunyai 3 pasang bidang sisi berhadapan yang kongruen,
Ø Balok mempunyai 12 rusuk,
Ø 4 buah rusuk yang sejajar sama panjang,
Ø Balok mempunyai 8 titik sudut,
Ø Jaring-jaring balok berupa 6 buah persegi panjang.
Rumus Luas Permukaan Balok
L = 2 x [ (p x l) + (p x t) + (l x t) ]
Keterangan:
t : tinggi balok
p : panjang balok
l : lebar balok
Rumus Volume Balok
V = p x l x t
Keterangan:
t : tinggi balok
p : panjang balok
l : lebar balok
PRISMA

Ciri-ciri PRISMA, antara lain:
Ø Prisma merupakan bangun ruang yang alas dan atasnya kongruen dan sejajar,
Ø Rusuk prisma alas dan atas yang berhadapan sama dan sejajar,
Ø Rusuk tegak prisma sama dan sejajar,
Ø Rusuk tegak prisma tegak lurus dengan alas dan atas prisma,
Ø Rusuk tegak prisma disebut juga tinggi prisma,
Ø Prisma terdiri dari prisma segitiga dan prisma beraturan.
Ø Prisma segitiga mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen.
Ø Prisma segitiga mempunyai 5 sisi.
Ø Prisma segitiga mempunyai 9 rusuk
Ø Prisma segitiga mempunyai 6 titik sudut
Ø Jaring-jaring prisma segitiga berupa 2 segitiga, dan 3 persegi panjang.
Rumus Luas Permukaan Prisma Segitiga
L = Keliling ∆ x t x ( 2 x Luas ∆)
Volume Prisma Segitiga
V = Luas Alas x t
Keterangan :
L : luas permukaan
∆ : alas dan atas segitiga
t : tinggi prisma
V : Volume
Luas Alas : Luas ∆ = ( ½ a x t )
t : tinggi prisma
LIMAS
Ciri-ciri LIMAS,antara lain:
Ø Limas adalah bangun ruang yang mempunyai bidang alas segi banyak dan dari bidang alas tersebut dibentuk suatu sisi berbentuk segitiga yang akan bertemu pada satu titik,
Ø Nama limas ditentukan oleh bentuk alasnya,
Ø Limas beraturan yaitu limas yang alasnya berupa segi beraturan,
Ø Tinggi limas adalah garis tegak lurus dari puncak limas ke alas limas,
Ø Macam-macam bentuk limas, antara lain:
1. Limas segitiga ( alasnya berbentuk segitiga )

2. Limas segiempat ( alasnya berbentuk segi empat )

3. Limas segilima ( alasnya berbentuk segilima )

4. Limas segienam ( alasnya berbentuk segienam )

|
Nama Limas
|
Sisi
|
Rusuk
|
Titik Sudut
|
| Limas Segitiga |
4
|
6
|
4
|
| Limas Segiempat |
5
|
8
|
5
|
| Limas Segilima |
6
|
10
|
6
|
| Limas Segienam |
7
|
12
|
1
|
L = luas alas + luas selubung limas
Rumus Volume Limas
V = 1/3 ( luas alas x t )
Keterangan:
t : tinggi limas
TABUNG

Ciri-ciri TABUNG, antara lain:
Ø Tabung merupakan bangun ruang berupa prisma tegak dengan bidang alas dan atas berupa lingkaran,
Ø Tinggi tabung adalah jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas,
Ø Bidang tegak tabung berupa lengkungan yang disebut selimut tabung,
Ø Jaring-jaring tabung tabung berupa 2 buah lingkaran dan 1 persegi panjang.
Rumus Luas Permukaan Tabung
L = 2 x ( π r2 ) + π d x t
Rumus Volume Tabung
V = 1/3 (luas alas x t)
Keterangan:
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi tabung
V : Volume
luas alas : π r2
KERUCUT

Ciri-ciri KERUCUT,antara lain:
Ø Kerucut merupakan bangun ruang berbentuk limas yang alasnya berupa lingkaran,
Ø Kerucut mempunyai 2 sisi,
Ø Kerucut tidak mempunyai rusuk,
Ø Kerucut mempunyai 1 titik sudut,
Ø Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga.
Rumus Luas Permukaan Kerucut
L = π r2 + π d xt
Rumus Volume Kerucut
V = 1/3 ( π r2 x t )
Keterangan:
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi kerucut
BOLA

Ciri-ciri BOLA, antara lain:
Ø Bola merupakan bangun ruang berbentuk setengah lingkaran diputar mengelilingi garis tengahnya,
Ø Bola mempunyai 1 sisi dan 1 titik pusat,
Ø Sisi bola disebut dinding bola,
Ø Bola tidak mempunyai titik sudut dan rusuk,
Ø Jarak dinding ke titik pusat bola disebut jari-jari,
Ø Jarak dinding ke dinding dan melewati titik pusat disebut diameter.
Rumus Luas Permukaan Bola
L = 4 π r2
Rumus Volume Bola
V = 4/3 π r3
Keterangan:
L : luas permukaan
V : Volume
r : jari-jari bola
π : 22/7 atau 3,14
Rabu, 27 Maret 2013
Properties of Quadrilateral
SIFAT_SIFAT BANGUN DATAR
Bangun datar merupakan sebuah bangun berupa bidang datar yang dibatasi oleh beberapa ruas garis. Jumlah dan model ruas garis yang membatasi bangun tersebut menentukan nama dan bentuk bangun datar tersebut. Misalnya:
- Bidang yang dibatasi oleh 3 ruas garis, disebut bangun segitiga.
- Bidang yang dibatasi oleh 4 ruas garis, disebut bangun segiempat.
- Bidang yang dibatasi oleh 5 ruas garis, disebut bangun segilima dan seterusnya.
Bangun datar merupakan sebuah bangun berupa bidang datar yang dibatasi oleh beberapa ruas garis. Jumlah dan model ruas garis yang membatasi bangun tersebut menentukan nama dan bentuk bangun datar tersebut. Misalnya:
- Bidang yang dibatasi oleh 3 ruas garis, disebut bangun segitiga.
- Bidang yang dibatasi oleh 4 ruas garis, disebut bangun segiempat.
- Bidang yang dibatasi oleh 5 ruas garis, disebut bangun segilima dan seterusnya.
Jumlah ruas garis serta model yang dimiliki oleh sebuah bangun merupakan
salah satu sifat bangun datar tersebut. Jadi, sifat suatu bangun datar
ditentukan oleh jumlah ruas garis, model garis, besar sudut, dan
lain-lain.
Langganan:
Komentar (Atom)








